1. GİRİŞ
Robotların günlük hayat içinde gittikçe artan sayıları onların daha insansı özellikler kazanması ile sonuçlanmaktadır. Bu özelliklerden en önemlisi ise görmedir. İnsan, görme duyusu sayesinde sadece etrafını görmez, etrafını anlar ve vücut hareketlerini düzenleyen bir kapalı çevrim oluşturur. Bu kapalı çevrim hareketlerin daha düzgün ve daha hızlı olmasını sağlar. İnsana benzer şekilde robot manipülatörlerde görsel bilgiden kontrol bilgisinin elde edildiği kontrol yöntemi görsel servolama (GS) olarak adlandırılır. GS uygulamalarında görüntü-tabanlı görsel servolama (GTGS) 3B uzayda duruş kestirimi gerektirmediğinden popüler GS yaklaşımlarından biridir.
Bu proje çalışması klasik GTGS’nın baş etmek zorunda kaldığı sorunlar üzerine odaklanmıştır. Bu sorunlar sırasıyla etkileşim matris tersi tekilliği, sabit kazanca bağlı yakınsama hızı, öznitelikleri görüş alanı içinde tutma ve bozuculara karşı gürbüzlük şeklinde sıralanabilir. GTGS için tasarlanacak kinematik kontrolcü, etkileşim matrisi adı verilen ve 3B uzaydaki noktanın görüntü düzlemine aktarımını sağlayan dönüşüm matrisinin yalancı tersine ihtiyaç duymaktadır. Bu ters alma işlemi ise bazı GS senaryolarında mümkün olmayabilir ve GS çevriminin durmasına yol açar. Kinematik kontrolcü sabit bir kazanç değeriyle beraber robot manipülatör uç işlevcisinin doğrusal ve açısal hızlarını tasarlar fakat sabit kazanç değeri hız sınırları içinde yakınsama hızını da sınırlar. Klasik GTGS sistemleri görüntü tabanlıdır ve özniteliklerin görüntü düzlemindeki durumunu kullanır. Bununla beraber özniteliklerin görüş alanı dışına çıkabilme ihtimali ile ilgilenmez. Bu ihtimal ise eğrisel öznitelik yörüngesinin bulunduğu senaryolarda olası bir risktir. Bu sorunların yanında tüm GS sistemleri uygulamada görülen kamera kalibrasyon hataları ve görüntüde oluşan gürültüye bağlı öznitelik hataları ile baş etmek zorundadır.
Bu sorunların çözümüne dair literatürdeki çalışmalar analitik yöntemlere odaklanmaktadır ve her bir sorun ayrı çalışmalarda ele alınmıştır. Bununla beraber endüstriyel bir GS uygulaması bu sorunların hepsiyle aynı anda baş etmek zorundadır. Bu projede ise akıllı birimleri kullanan ve belirtilen sorunları tek bir sistemde çözmeyi hedefleyen bir GTGS sistemi önerilmiştir. Kullanılması planlanan akıllı birimler sırasıyla etkileşim matrisi tersine yakınsamak için yapay sinir ağları (YSA), radyal tabanlı ağlar (RTA), ekstrem öğrenen makinalar (EÖM), sabit kazanç yerine öznitelik hata ve hata değişimlerine bağlı uyarlanabilir kazanç değeri tanımlamak için bulanık mantık (BM) ve öznitelikleri görüş alanı içinde tutacak zıt yönlü hızlar tanımlayacak olan BM şeklindedir. Ayrıca, uyarlanabilir kazanç için kullanılan BM giriş olarak hareketlilik terimini de kullanarak manipülatörün tekil eklem konfigürasyonlarından uzak duracaktır. Bu birimlerin her biri bozuculara karşı analitik yöntemlerden daha az etkilendiklerinden önerilen sistem bozuculara karşı gürbüzlük sağlayabilecektir.
Önerilen sistem Bölüm 2’de belirtilen üç temel GS probleminin tek bir sistemde çözülmesini amaçlamaktadır. Önerilen sistem YSA, radyal tabanlı ağlar (RTA) gibi konvansiyonel akıllı yakınsama birimlerinin yanında ekstrem öğrenen makinalar (EÖM) gibi popülerleşen yeni nesil akıllı yakınsama birimlerini ve BM kullanan akıllı bir GTGS sistemi şeklindedir.
2. LİTERATÜR ÖZETİ
Görsel kılavuzlu robotlar giderek yaygınlaşırken bu robotların gördüklerini yorumlamaları ve bu yorumlama çerçevesinde hareket ederek görevlerini tamamlamaları önemli bir araştırma ve uygulama alanıdır. Görsel bilginin, kapalı çevrim bir kontrol sisteminde geri besleme sinyalleri olarak kullanılması görsel servolama (GS) olarak anılmaktadır (Chaumette ve Hutchinson, 2006). GS, eldeki kamera görüntüsünde tanımlı k öznitelik noktasının belirlenmesi ile oluşan s vektörünün istenen sabit durumda (s*) olması için hata sinyalini oluşturur ve bu hata sinyali ile kontrol yasasını tasarlayarak 3 boyutta istenen doğrusal ve açısal hızları tanımlar. GS, görüntüden doğrudan elde edilen s vektörünü kullanan görüntü-tabanlı görsel servolama (GTGS) ve görüntü ile robotun duruşundan yararlanılarak bulunan 3 boyutlu duruş kestirimlerini kullanan konum-tabanlı görsel servolama (KTGS) olarak ikiye ayrılır. GTGS, görüntü-konum dönüşüm adımlarını doğrudan yaparken KTGS aynı adımlarda duruş kestirimine ihtiyaç duymaktadır (Chaumette, 1998; Sharifi vd., 2011). Burada GTGS ve KTGS’nın karşılaştırması yapılacak olursa GTGS duruş kestirimine ihtiyaç duymaz ve kamera kalibrasyon hatalarından daha az etkilenirken etkileşim matrisinde tekillik görülebilir, derinlik bilgisi kestirilmelidir ve optimal dışı yörüngeler ortaya çıkabilir.
Bu tanımlamalarla kullanılan GTGS uygulama aşamasına geçtiğinde ise farklı problemlerle baş etmek zorundadır. Bunlardan ilki etkileşim matrisi tersinin eldesidir. Chaumette GS problemlerine dair yaptığı çalışmasında bazı GS senaryolarında etkileşim matrisinin yalancı tersinde tekillikler bulunabileceğini belirtmiş ve “Chaumette Bilmecesi” adını verdiği GS senaryosunu ortaya atmıştır (Chaumette, 1998).
Bu senaryoya göre nokta şeklindeki başlangıç öznitelikleri beyazla, hedef öznitelikler siyahla gösterilmektedir. Burada GTGS saf dönme işlemiyle elde edilebilir durumdadır ve bu da tekilliğe yol açmaktadır.
Bu tekilliklerden kaçınma için önerilen ilk yöntem tekilliğin yaklaştığı durumda KTGS’ya geçen ve melez GS yöntemleri olarak adlandırılan yöntemleri kullanmaktır (Malis vd, 1999; Corke ve Hutchinson, 2001). Bu yöntemler ayrıca KTGS’ye ihtiyaç duymaktadır. Bu problemden kaçınmanın başka bir yolu ise etkileşim matrisine yakınsamaya çalışmaktır. Etkileşim matrisine yakınsama ile ilgili çalışmalara bakıldığında Kumar ve Behera çalışmalarında stereo kameralı ele-karşılık-göz konfigürasyonlu fazlalıklı manipülatör için kendinden düzenlenen haritalar (Self Organizing Map-SOM) kullanarak etkileşim matris kestirimi yapmışlardır fakat çalışmada GTGS ve eldeki-göz konfigürasyonu ele alınmamıştır (Kumar ve Behera, 2010). Kosmopoulos, 6 eklemli bir manipülator için doğrusal bir öznitelik modeli ve en küçük kareler kestirimcisi ile bir kestirimci oluşturmaya çalışmıştır fakat kullanılan robot sadece tanımlı tek bir yörüngeyi takip etmek üzere tasarlanmıştır (Kosmopoulos, 2011). Sebastian vd. 3 eklemli ele-karşılık-göz konfigürasyonlu bir manipülator için herhangi bir yörünge tanımı ve başlangıç-hedef öznitelik vektör tanımı yapmadan Broyden, özyinelemeli en küçük kareler ve Kalman filtresini kullanarak kestirim yapmaya çalışmışlardır (Sebastian vd., 2009). Zhong vd. ise görüntü öznitelikleri ve bir önceki etkileşim matris kestirimi giriş olacak şekilde Elman sinir ağı ile çalışan gürbüz Kalman filtresi kullanarak kestirim yapmaya çalışmışlardır (Zhong vd., 2013). Bu çalışmada gürültüye karşı gürbüzlüğün çok sınırlı olduğu ve hız kontrolcüsü üzerinde herhangi bir değişiklik yapılmadığı görülmektedir. Başka bir çalışmalarında ise etkileşim matrisine yakınsamada Kalman filtresinin gürbüzlüğünü artırmak için yapay sinir ağı (YSA) destekli Kalman filtresi kullanmışlardır fakat bu çalışmada da uç işlevcisinin hızları göz ardı edilmiştir (Zhong vd., 2015). Gonçalves vd. ise ele-karşılık-göz konfigürasyonlu robotlar için robotun eklem açılarını ve özniteliklerdeki değişimleri kullanarak robotun hız değerlerini ters bulanık modelleme ile bulmaya çalışmışlardır (Gonçalves vd., 2008). Kullandıkları bulanık model öğrenme yeteneğine sahip değildir ve çalışmada ele-göz konfigürasyonu ve KTGS göz önünde bulundurulmuştur. Bu yaklaşımın haricinde etkileşim matrisini tamamen ortadan kaldıran çalışmalar da literatürde mevcuttur. Miljkovic vd. etkileşim matrisi olmadan klasik GS’da bir YSA pekiştirme temelli bir kontrolcüyle bir melez GTGS sistemi önermişlerdir (Miljkovic vd., 2013). Çalışmalarında görüntü düzlemini eyleyici komutlarına Q-öğrenme ve SARSA ile haritalamışlar fakat eyleyici komut yaklaşım sonuçlarını göstermemişlerdir. Ayrıca elde ettikleri hız sinyalleri büyük çatırtılar içermektedir.
GS uygulamalarında ortaya çıkan ikinci problem ise kazanç değerinin tüm GS çalışması boyunca sabit tutulmasıdır. GS çevrimi tanımlanırken robot manipülatörün ne kadar hızlı yakınsayacağını belirleyen, bunun yanında manipülatöre ait hız sınırlarının göz önünde bulundurulması gereken bir kazanç değeri belirlenmelidir. Bu değerin belirlenmesinde analitik bir ifade yerine kullanıcı tecrübesi önem kazanmaktadır. Bunun için değişen bir kazanç önerilebilir fakat ani değişen kazanç değerlerinin ani hız değişimlerine sebep olacağından değişimin olabildiğince yumuşak yapılması gerekmektedir. Kermorgant ve Chaumette çalışmalarında eldeki-göz ve ele-göz konfigürasyonlu kameralardan ve manipülatör sisteminin kısıtlarından oluşan bir öznitelik setini kullanan bir çoklu-sensör manipülatör sistemi tasarlamıştır (Kermorgant ve Chaumette, 2014). Çalışmalarında ağırlıklandırılmış terimlerle bir doğrusal karesel kontrolcü önermişler ve önerdikleri sistemi kısıtları içinde tutabilmek için uyarlanabilir bir kazanç değeri önermişlerdir.
GS uygulamalarında karşılaşılan yaygın sorunlardan biri de özniteliklerin görüş alanı dışına çıkmasıdır (Chaumette, 1998). Özniteliklerin görüş alanından çıkması GS’nin yakınsayamaması veya tamamen durması gibi katastrofik sonuçlar doğurabilmektedir. Özniteliklerin görüş alanı dışına çıkması durumu Z derinlik kestirimine ait hatanın büyük olması, özniteliklerin görüntü kenarlarına çok yakın olması veya KTGS’nın tek başına kullanılması durumunda ortaya çıkmaktadır. Öznitelikleri görüş alanı içinde tutma için Corke ve Hutchinson robot manipülatörler için çarpışmadan kaçınma yöntemlerinde yararlanmış ve öznitelikleri görüntü düzlem sınırlarından öteleyen türevlenebilir bir potansiyel fonksiyon tanımlamışlardır (Corke ve Hutchinson, 2001). Bu fonksiyon özniteliklerin görüntü koordinatlarına bağımlı olan karesel bir fonksiyondur. Çalışmalarında bu alanın yerel minimuma sebep olabileceğinden bahsedilmiştir. Gans vd. ise özniteliklerin ortalamasını temel alan bir görev fonksiyonu tanımlamış ve bunu bir mobil robot üzerinde uygulamışlardır (Gans vd., 2011). Tasarlanan sistem sadece mobil robotlara uygulanabilir haldedir. Ayrıca çalışmada piksel cinsinden ortalama hataları oldukça yüksektir ve hızın zamana göre değişimleri göz ardı edilmiştir. Chesi vd. özniteliklerin görüş alanı sınırına göre durumlarına bakarak doğrusal ve açısal hızları değiştiren veya geriye doğru hareket eden bir görüş alanı koruma sistemi önermişlerdir (Chesi vd., 2004). Bu iki seçenek arasındaki geçişler hızlarda yüksek çatırtıya sebep olmaktadır. Ayrıca çalışmada geriye doğru hareketin hedeften ıraksamaya sebep olabileceği belirtilmiştir.
Bu literatür özetine ek olarak yapılan çalışmaların yukarıda bahsedilen problemlerden çoğunlukla birine odaklandığı, diğerlerine odaklanmadığı, bununla birlikte her üç probleminde gerçek zamanlı bir GS uygulamasında karşılaşılabileceği belirtilmelidir. Bu yapılan çalışmalar bu problemlerin çözümünde yeni yaklaşımlara ihtiyaç olduğunu göstermektedir. Bu proje çalışmasında bahsedilen üç problemin çözümüne akıllı yapılar kullanılarak çözümler getirilmeye çalışılmıştır. İlk olarak yalancı ters etkileşim matrisinin analitik olarak tanımlanmasına bağlı tekillik probleminin akıllı yakınsayıcı kullanılarak çözülmesine odaklanılmıştır. İkinci problemin çözümü için kazanç değerinin çalışma boyunca değişken olmasıyla hız limitleri içinde daha hızlı yakınsama sağlayan bulanık mantık (BM) tabanlı bir kinematik kontrolcü tasarımına odaklanılmıştır. Son olarak üçüncü problemin çözümü için görüş alanının bölgelere ayrılması ve bölgelere ve yaklaşılan görüntü sınırına göre bir bulanık mantık birimiyle tanımlı zıt yönlü bir hızla öznitelikleri görüntü merkezine sürükleyen bir çözüme odaklanılmıştır. Ayrıca bu problemlere getirilen çözümlerin beraber çalışması ve kamera kalibrasyonuna bağlı kamera parametrelerindeki hatalara ve görüntüye bağlı olarak özniteliklerde görülebilecek gürültülere karşı gürbüz olması projede önerilen sistemin amaçlarındandır.
3. Önerilen Akıllı GTGS Sistemi
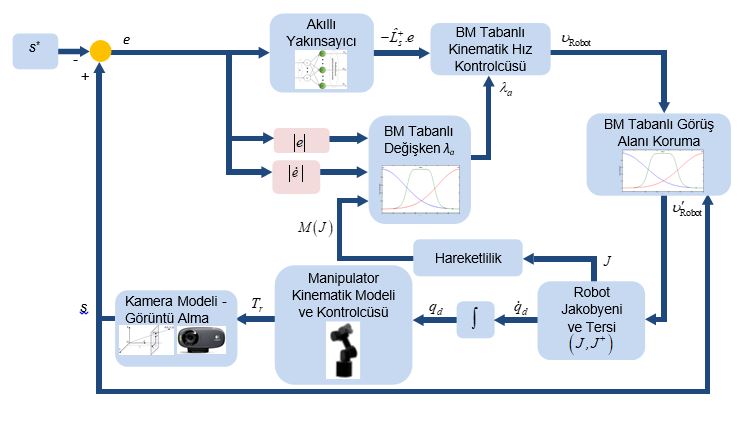
Önerilen sistemin genel gösterilimi Şekil 1’de verilmiştir.
Şekil 1. Önerilen akıllı GTGS sistemi
Önerilen sistemin ilk adımını görüntü alma ve görüntü bozulmalarının (distorsiyon) giderilmesi oluşturmaktadır. Kullanılan kameraya bağlı olarak alınan görüntüde oluşacak bozulmalar çıkarılacak görüntü özniteliklerinde değişikliğe sebep olabilir. Örneğin nokta şeklinde bir özniteliğin görüntü düzlemine izdüşümleri görüntü bozulmalarından dolayı etkilenecektir. Bu sebeple kameranın GS çevrimine sokmadan önce mutlaka kalibre edilmesi gerekmektedir. Bunun için bir satranç tahtası görseli ile kameraya belli mesafelerden belirli dönmeler ve farklı perspektiflerle görüntü alınarak bu görüntü üzerinde satranç tahtasındaki kare köşe noktaları belirlenerek kamera matrisi elde edilmeli, elde edilen kamera matrisine dair parametrelerde görüntüde düzeltme yapılmalıdır. Projede kullanılan kamera görüntüsünde bu düzeltme işlemleri yapılmıştır.
Alınan görüntüden nokta şeklinde öznitelik çıkarımı sistemin ikinci adımını oluşturmaktadır. Bu adım için 3 adet nokta için öznitelik çıkartılması uygun görülmüştür. Burada 6 serbestlik dereceli bir robot manipülatör için en az 3 noktaya dair öznitelik gerektiği belirtilmelidir (Chaumette ve Hutchinson, 2006). Devamında hedef öznitelikler ile mevcut öznitelikler arasındaki fark ard arda bağlanarak hata vektörü elde edilmektedir.
Önerilen sistemde akıllı bir yakınsayıcı ile etkileşim matrisine yakınsama önerilmiştir. Burada doğrudan etkileşim matrisine yakınsamanın getirdiği bir zayıflıktan bahsetmek gerekmektedir. Etkileşim matrisinin boyutu ile tanımlandığından öznitelik sayısına göre yakınsayıcı çıkışı tekrar ayarlanmalıdır. Bunun yerine değerine yakınsamak sabit sayıda çıkışı sağlamaktadır. Burada ağ girişi her bir özniteliğe dair hata vektörü olacaktır. Ağdan beklenen ise kestirilmiş etkileşim matrisi tersi ile hata vektörü çarpımının oluşturduğu fonksiyona yakınsamasıdır. Bu sayede öznitelik nokta sayısıyla değişen etkileşim matrisi eleman sayısı yerine öznitelik nokta sayısından bağımsız, sadece doğrusal ve açısal hızlara etkiyen 6 çıkış tanımlanacaktır.
Sistemde akıllı yakınsayıcı olarak uygun boyutta YSA, RTA, EÖM, DVM ve ANFIS kullanılmıştır. Bu ağların eğitimi için klasik GTGS (sabit kazanç varken ve görüş alanı koruması olmadan) ile farklı başlangıç konum ve duruşlarında farklı başlangıç öznitelikleri için elde edilen veriler alınmış ve eğitim için kullanılmıştır.
4. Önerilen Akıllı GTGS Sistemine Dair Gereçler
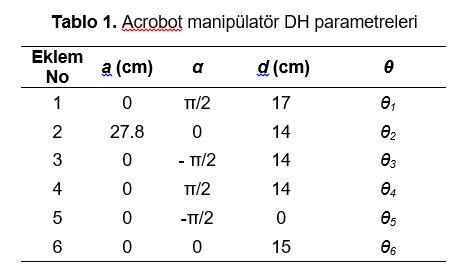
Önerilen akıllı GTGS sisteminde kullanılan Acrobot isimli robot manipülatör ACROME firması tarafından geliştirilmiş olup 6 döner eklemli, ± 0.1 mm hassasiyete, tam açık durumda 760 mm uzunluğa ve 1 kg yük taşıma kapasitesine sahip bir robot manipülatördür (Acrome, 2020). Manipülatörün sabitlenmiş görüntüsü ve eklem dönüş yönleri Şekil 2’de gösterilmektedir. Robota dair DH parametreleri ise Tablo 1’de verilmektedir.
Robotun görüntü almak için uç işlevcisine monte edilen kamera ise Logitech CH310 HD kameradır. Kullanılan kamera 1024×768 çözünürlükte 30 FPS görüntü aktarımı yapabilmektedir. Kullanılan kamera, manipülatör uç işlevcisi olarak Şekil 2’de görülmektedir.
Şekil 2. Acrobot robot manipülatör ve Logitech CH310 kamera
Robot manipülatörün her bir eklemindeki Dynamixel PRO serisi akıllı servo motorlar fırçasız veya çekirdeksiz DA motor, redüktör ve sürücüyü bir araya getirmekte, bu sayede sadece USB ve güç bağlantısıyla doğrudan programlamaya izin vermektedir. Acrobot eklemlerinde Dynamixel Pro L54, H54 ve M42 serisi motorlar kullanılmış olup bu akıllı servoların iç yapısına dair örnek bir görünüm Şekil 3’de verilmektedir (Robotis, 2020).
Şekil 3. Dynamixel Pro serisi akıllı servo motor iç yapısı
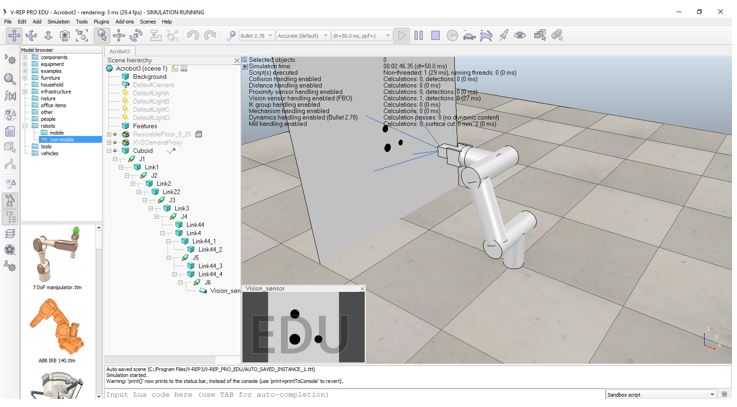
Yapılan gerçek zamanlı gerçekleme çalışmalarına geçmeden önce MATLAB Robotics Toolbox ve V-REP kullanılarak proje çalışmasına altyapı oluşturması için yapılmış benzetim ortamına dair bir örnek Şekil 4’te gösterilmektedir. Burada görüntü alma ve robot mekanik benzetimi V-REP üzerinden yapılırken ters kinematik hesap MATLAB ortamında yapılmaktadır. MATLAB ortamında elde edilen eklem açıları V-REP’e gönderilmektedir. Bu benzetim ortamı özellikle düz ve ters kinematik etkilerin görülmesinde ve öznitelik noktalarının eşleştirilmesinde projeye kolaylıklar sağlamıştır.
Şekil 4. MATLAB- VREP Acrobot benzetim ortamı
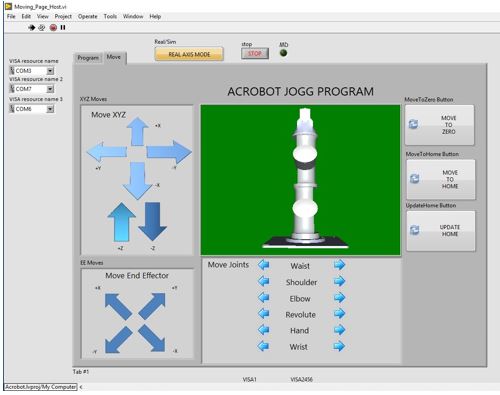
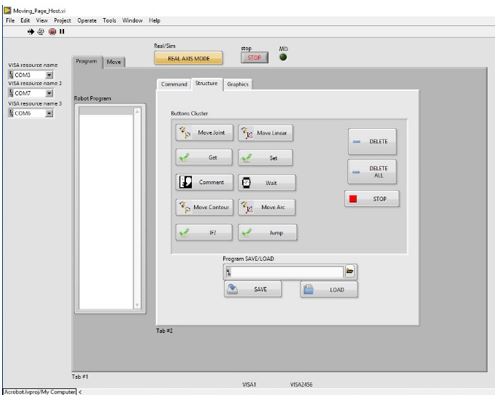
Proje çalışmasında yazılım ortamı olarak MATLAB-Simulink (R2017b) Robotics Toolbox 9.0, Neural Network Toolbox, Fuzzy Logic Toolbox ve NI LabVIEW 2018, NI Dynamixel API, NI Vision for LabVIEW, NI IMAQ VI, NI Vision Acquisition Express VI yazılımlarından yararlanılmıştır. Robot manipülatörün kullandığı akıllı servoların her ne kadar MATLAB programlama desteği bulunsa da Acrobot robot manipülatörün programlama ortamının projenin satın alma aşamasında üretici firma tarafından sadece LabVIEW aşaması tamamlanmış, MATLAB kodlarının yazım aşamasının devam ettiği firma tarafından belirtilmiştir. Bununla beraber satın alma aşamasında döviz kurundaki yükselme sebebiyle maliyeti düşürmek adına firma tarafından Acrobot robot manipülatörün motor sürme için kullanılan haberleşme yönteminde değişikliğe gidilmiştir. Bu yöntemde robotun her bir eklemine dair 6 servo motor 3 ayrı USB arayüzü tarafından sürülmüştür. Bu sürme için USB çoklayıcı kullanılarak bilgisayar ile haberleşme sağlanmıştır. LabVIEW, sağladığı multitasking özelliği ile çoklu USB haberleşmesine zaman paylaşımı (time sharing) ile imkan sağlamaktadır. Diğer taraftan Acrobot robot manipülatörün MATLAB kodları yazımı tamamlandığında (Mayıs 2019) MATLAB’ın çoklu USB haberleşmeye izin vermediğinden bu konfigürasyona doğrudan MATLAB desteği sağlanamayacağı firma tarafından belirtilmiştir. Acrobot’un Labview üzerinde tanımlı programlama arayüzüne dair örnek görünümler Şekil 5’ta verilmiştir.
(b)
(d)
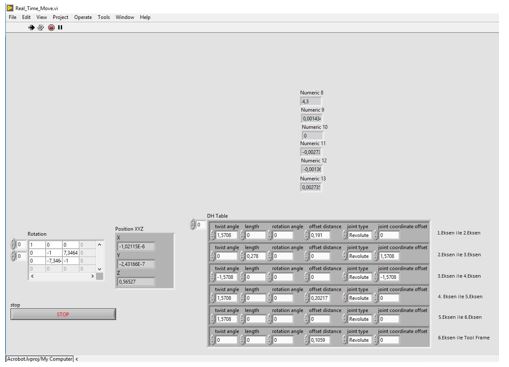
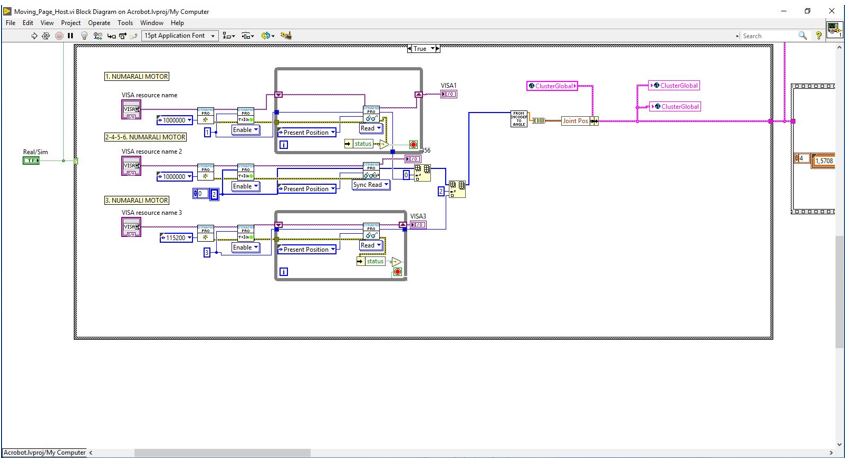
Şekil 5. Acrobot LabVIEW programlama arayüzü
(a) 3B animasyon ve grafiksel programlama ortamı (b) Komutlarla programlama ortamı (c) DH tablosu ve eklem açıları (d) Motor kontrol blok diyagramından bir kesit
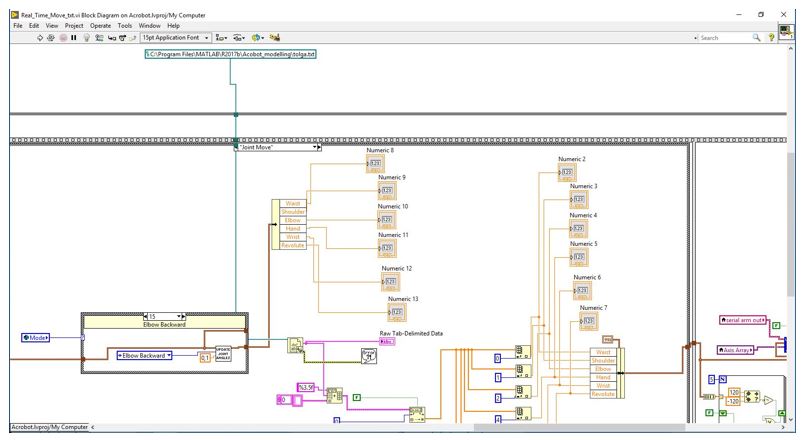
Robot manipülatörü kontrol eden yazılımın LabVIEW ortamında bulunması ve bu ortamında YSA gibi yapılara destek vermemesinden dolayı projenin yürütülmesi amacıyla LabVIEW-MATLAB haberleşmesine ihtiyaç duyulmuştur. MATLAB üzerinde gerekli hesaplamalardan sonra robota dair 6 eklem açısının LabVIEW’e gönderilmesi gerekmektedir. Açıların geribeslemeli kontrolü ise akıllı servo üzerindeki PID kontrolcü tarafından yapılmaktadır. LabVIEW ve MATLAB birbirlerine rakip programlama ortamları olduklarından doğrudan gerçek zamanlı haberleşme destekleri bulunmamaktadır. Proje çalışmasında ilk olarak bu iki ortam arasında TCP-IP üzerinden haberleşme denenmiştir. TCP-IP karşılıklı el sıkışma ve veri gönderim-alım tasdiki (acknowledgement) içerdiğinden her bir eklem açı verisi ancak 1 saniyede, toplamda 6 eklem açısı 6 saniyede iletilebilmiştir. Bu durum da gerçek zamanlı çalışmaya engel olduğundan daha pratik bir çözüm getirilmiş ve MATLAB’da GTGS hesapları sonrası eklem açılarının bir .txt dosyasına yazılması sağlanmış, LabVIEW tarafında da bu dosyanın anlık olarak okunması sağlanmıştır. Bu yazma-okuma işleminde sabit adımlı bir döngü sağlanamasa da yaklaşık 1 saniyelik bir döngü süresi elde edilebilmiştir. Oluşturulan bu haberleşme yapısına dair LabVIEW blok diyagramına dair bir kesit Şekil 6’da verilmiştir.
Şekil 6. MATLAB-LabVIEW haberleşmesine dair blok diyagram kesiti
1 sn.’lik çevrim süresi gerçek zamanlı bir robot manipülatörün çalışması için uygun olmayacağı aşikardır. Çevrim süresini sabitlemek için görüntü alma-GTGS aşamaları için sabit adımlı (sabit zaman) sayısal çözümleme kullanılmış, bu sebeple de 1 sn.’lik çevrim süresi elde edilmiştir. Literatürde geçerli çalışmalar incelendiğinde ise sabit adımla çevrim süresi yerine iterasyon sayısına odaklanan çalışmaların öne çıkmaktadır (Corke ve Hutchinson, 2001; Malis vd. 1999; Chaumette, S. Hutchinson, 2007). Bu sebeple MATLAB kodlarında yapılan değişikliklerle sabit adım yerine zamanlamayı beklemeyen sürekli zamanlı bir kontrol sistemi oluşturulmuş, projedeki sonuçlar da iterasyon sayısı olarak verilmiş ve değerlendirilmiştir.
MATLAB-LabVIEW haberleşme için gerekli yapı Şekil 7’de gösterilmektedir. LabVIEW’e yollanan q(i) eklem açıları ile robot manipülatörün hareketi sağlanmaktadır. Hareket sonrasında uç işlevciye bağlı kameradan MATLAB ile görüntü alınmakta ve MATLAB içindeki kapalı GTGS döngüsüne sokulmaktadır.
Şekil 7. MATLAB-LabVIEW haberleşme döngüsü
PROJE TRDİZİN SAYFASI
PROJE SONUÇ RAPORU
KAYNAKLAR
Acrome, “ACROBOT, 6 DOF Robotic Arm for research and teaching”, https://acrome.net/6-dof-robotic-arm, Son erişim tarihi: 15.01.2020
Chaumette, F., Hutchinson, S., 2006, “Visual servo control. I. Basic approaches”, IEEE Robot. Autom. Mag., 13, 82–90.
Chaumette, F.,1998, “Potential problems of stability and convergence in image-based and position-based visual servoing”, sayfa:66-78, Lect. Notes Control Inf. Sci.
Chesi, G., Hashimoto, K., Prattichizzo, D., Vicino, A., 2004, “Keeping features in the field of view in eye-in-hand visual servoing: A switching approach”, IEEE Trans. Robot. 20, 908–913.
Chesi, G., Hung, Y.S., 2007, “Global path-planning for constrained and optimal visual servoing”, IEEE Trans. Robot., 23, 1050–1060.
Corke, P.I., Hutchinson, S.A., 2001, “A new partitioned approach to image-based visual servo control”, IEEE Trans. Robot. Autom., 17,507–515.
Esener, İ. I., Ergin, S., Yuksel, T. 2017, “A New Feature Ensemble with a Multistage Classification Scheme for Breast Cancer Diagnosis”, Journal of Healthcare Engineering,1-15.
Gans, N.R., Hu, G., Nagarajan, K., 2011, “Keeping multiple moving targets in the field of view of a mobile camera”, IEEE Trans. Robot., 27, 822–828.
Gonçalves, P.J., Mendonça, L.F., Sousa, J.M.C., Pinto, J.R.C., 2008, “Uncalibrated eye-to-hand visual servoing using inverse fuzzy models”, IEEE Trans. Fuzzy Syst. 16, 341–353.
Heikkila, J., Silven, O., 1997, “A four-step camera calibration procedure with implicit image correction”, IEEE International Conference on Computer Vision and Pattern Recognition.
Huang, G., Zhou, H., Ding, X., Zhang, R., 2012, “Extreme learning machine for regression and multiclass classification,” IEEE Trans. Syst. Man, Cybern. B Cybern., 42, 513–529.
Jang, S. R., Sun, C. T. ,1997, Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence. Prentice-Hall.
Kermorgant, O., Chaumette F., 2014, “Dealing with constraints in sensor-based robot control”, IEEE Trans. Robot., 30, 244–257.
Kosmopoulos, D.I., 2011, “Robust Jacobian matrix estimation for image-based visual servoing”, Robot. Comput. Integr. Manuf., 27, 82–87.
Kumar, P.P., Behera, L., 2010, “Visual servoing of redundant manipulator with Jacobian matrix estimation using self-organizing map”, Rob. Auton. Syst., 58, 978–990.
Malis, E., Chaumette, F., Boudet, S., 1999, “2 1/2 D visual servoing”, IEEE Trans. Robot. Autom., 15, 238–250.
Mezouar, Y., Chaumette, F., 2002, “Path planning for robust image-based control”, IEEE Trans. Robot. Autom., 18, 534–549.
Miljkovic, Z., Mitic, M., Lazarevic, M., Babic, B., 2013, “Neural network reinforcement learning for visual control of robot manipulators”, Expert Systems with Applications, 40, 1721–1736.
Gonzales, R.C., Woods, R.E., 2008, Digital Image Processing, 3. Baskı, Prentice-Hall.
Robotis, ”Dynamixel Pro e-manual”, http://emanual.robotis.com/docs/en/dxl/pro/, Son erişim tarihi: 16.01.2020
Haykin, S., 1998, Neural Networks: A Comprehensive Foundation, 2. Baskı, Prentice Hall.
Sebastian, J.M., Pari, L., Angel, L., Traslosheros, A., 2009, “Uncalibrated visual servoing using the fundamental matrix”, Rob. Auton. Syst., 57, 1–10.
Sharifi, F. J., Deng, L., Wilson, W.J., 2011, “Comparison of basic visual servoing methods”, IEEE/ASME Trans. Mechatronics. 16, 967–983.
Vapnik, V., 1995, The Nature of Statistical Learning Theory. Springer, New York.
Yoshikawa, T., 1985, “Manipulability of robotic mechanisms”, Int. J. Rob. Res. 4, 3–9.
Zhao, Z.Y., Tomizuka, M., Isaka, S., 1993, “Fuzzy Gain Scheduling of PID Controllers”, IEEE Trans. Syst. Man Cybern., 23, 1392–1398.
Zhong, X., Zhong, X., Peng, X., 2013, “Robust Kalman filtering cooperated Elman neural network learning for vision-sensing-based robotic manipulation with global stability”, Sensors, 13, 13464–13486.
Zhong, X., Zhong, X., Peng, X., 2015, “Robots visual servo control with features constraint employing Kalman-neural-network filtering scheme”, Neurocomputing, 151, 268–277.