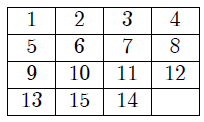
Bir kral ele geçen esirlere şu şekilde bir öneri sunmuştur. “Daire şeklinde dizilin. İçinizden rastgele birine bir kılıç vereceğim. Bu birinci olsun. Kılıcı verdiğim hemen solundakini öldürecek ve kılıcı ölen esirin solundakine yani üçüncüye verecek. Kılıcı alan solundakini öldürüp kılıcı öldürdüğünün yanındakine verecek. Bu şekilde 1 kişi kalana kadar devam edecek. Son kalan esiri serbest bırakacağım.” Buna göre toplam 1000 esir varsa kaçıncı kurtulacaktır?

Çözüm şu şekilde : Eğer esir sayısı 2 nin bir üssü olursa daima kralın kılıcı ilk verdiği esir kurtulacaktır. Örneğin 64 esir olsun. İlk önce ((64)/2)=32 kişi ölecek kılıç tekrar birinciye gelecektir. ((32)/2)=16 kişi ölecek sıra tekrar birinciye gelecek. En son kılıç birincinin eline gelecek ve iki kişi kalacaklar. Yani birinci kurtulacak. Genel olarak n kişi varsa n den en yakın 2 nin kuvvetini çıkarıyoruz. Kalan k ise bu durumda 2k+1 numaralı kişi kurtulur. Örnek olarak 1000 kişi için çözüm yaparsak: 1000 den en yakın 2 nin kuvvetini atalım 1000-2⁹=488 olduğundan 2×488+1= 977 numaralı esir kurtulacaktır. Çözümün neden bu olduğunu okuyucuya bırakıyorum kasten. Asıl sormak istediğim problemi soramam yoksa.

Gelelim asıl mevzuya. Milattan sonra 66-73 yılları arasında Roma imparatoru Neron öldürülmüş ve Roma imparatorluğu bir iç savaş yaşamaktaydı. Neron zamanında Roma yı mamur etmek için başlatılan seferberlik Roma yı adeta bir inşaat alanına çevirmekle kalmamış bunun altından kalkabilmek için vergiler olabildiğinde artırılmıştı. Günümüzde İsrail olarak bilinen Judea’nın Romalı valisinin vergileri artırmasını bahane eden yahudiler iç savaşı da fırsat bilip isyan ettiler. Judea topraklarındaki tüm Romalılar Kudüs dışına çıkarılmış isyan durdurulamaz bir hal almıştı. Bundan 6 ay sonra, 30 bin Roma askeri isyanı bastırmak için gönderildi. M.S. 66 yılının kışında, Yahudi direnişçiler Beyt Horon da 30 bin askerden 6 bin kadarını öldürdü. Beyt Horon katliamı Roma ordusunun isyan eden bir eyalete karşı aldığı en büyük yenilgiydi. Roma, isyanın İmparatorluğun diğer bölgelerine sıçramasından korkuyordu. Galile’deki Yahudi halkının direniş liderliğini Josephus adında zeki bir yahudi yapmaktaydı. Görevi Roma saldırısına karşı direnişi hazırlamaktı. Bu sırada Romalıların kıskacı giderek daralıyor koca Roma ordusunun dörtte biri Galile’ye doğru yaklaşıyordu. Çetin bir kuşatmanın ardından Romalı askerler Josephus’un savunduğu kaleye girmeyi başardılar. Josephus ve beraberindeki 41 kişi kale içindeki o karışıklıkta bir su kuyusuna girip saklandılar. Ancak bir şekilde, Josephus’un yerini Romalı askerler öğrendi. Romalı komutan kuyuya saklananlara teslim olmaları halinde hayatlarını bağışlama vadinde bulundu. Josephus teslim olma taraftarı olmasına rağmen beraberindeki hiçkimse teslim olmaya yanaşmıyordu. Josephus’ un teslim olma fikrini hainlikle eşdeğer görüyorlar, teslim olmaktansa kendimizi öldürelim diyorlardı. Fakat Josephus’ un kendini öldürmeye veya hain olarak anılmaya hiç niyeti yoktu. Fakat arkadaşlarını da ikna edemeyince aklına başka bir şey geldi. İçlerinden biri vardı ki Josephus, O’nun da ölmesini istemiyordu. Şöyle bir teklifte bulundu : “Kişinin kendini öldürmesi Tanrı’ya hakarettir. Bunun yerine herkes bir başkası tarafından öldürülsün. Kimin kim tarafından öldürüleceğini ise şöyle belirleyelim. Herkes çember şeklinde dizilsin. Herhangi bir kişiden itibaren (bu saymaya başlanılan kişiye birinci diyelim) sol tarafa, doğru her üçüncü kişi sağındaki tarafından öldürülecek. (Yani üçüncü kişi ölecek.)” Bu şekilde sırası ile 3., 6., 9., … öldürüldü ta ki iki kişi kalana kadar. İşin ilginç yanı -her nasılsa- son kalan iki kişi Josephus ve yakın arkadaşı Yaakov oldu. Josephus bilge bir adamdı. Bu yüzden son kalan iki kişinin kendisi ve arkadaşı Yaakov olmasını bir şekilde ayarlaması mümkündü. Josephus daha sonra bu kurtuluşu Tanrı’nın isteği olarak nitelendirecekti. Acaba Josephus ve Yaakov kaçıncı sırada idiler? Ya da herhangi sayıda kişi olduğunda saymaya ilk başladığımız birinci ise kurtulan iki kişi kaçıncı numaralar olur?

Samuel Loyd, 1841-1914 yılları arasında yaşamış, Amerikalı ünlü bir satranç ve bulmaca ustasıdır. Büyük bir bulmaca ustası olan Martin Gardner O’nu “Amerika’nın en büyük bulmaca ustası” ve “bulmacanın prensi” olarak tanımlar. Bununla birlikte yalanları ve benciliği ile de ünlü olan Sam Loyd hakkında Martin Gardner, ” ve ayrıca üçkağıtçı” diye bahseder. Zira başkalarına ait bulmacaları kendi bulmacası gibi sunarak kendi ününü artırmıştır. İşte bu bulmacalardan biri de Cyclopedia of Puzzles adlı kitabında yer verdiği 14-15 bulmacasıdır. Bu bulmaca aslında Noyes Chapman’a aittir. 1880 yılında ilk yayınlandığında Amerika ve Avrupa’da büyük bir merak estirmiştir.

1 den 15 e kadar numaralandırılmış 15 adet parça yap-boz şeklindeki tahtaya şekildeki gibi dizilmiştir. (Resim oluşturma şeklindeki yap-bozlar gibi). Her bir parça sağa-sola veya yukarı-aşağı doğru ,eğer hareket ettireceğiniz yer boş ise, hareket etmektedir. Parçalar 1 den 15 e kadar dizilebilir mi? Bu soruyu çözene o günün parasıyla tam 1000 dolar verileceği vadedilmişti.

1 Nisan 1946 da, Erewhon Daily Howler gazetesi, okuyucularına “Meşhur astrolog Profesör Umbigo 2141 yılı dünyanın sonu olacak dedi” diye duyurdu. Gazeteye göre, Profesörün önsezisi matematiksel bir ispata dayanıyordu. Profesörün bulduğu matematiksel ispat şöyleydi:

eşitliğinin için aylarca bilgisayarla yapılan incelemeler sonucu daima 1946 ile tam bölündüğü bulunmuştu. Bu sayılar rastgele sayılar değildi. Hepsi dünyada önemli tarihleri gösteriyordu. Şöyle ki, 1492, 1770 ve 1863 sayıları dünyada önemli üç tarihi göstermekteydi. Bunlar sırasıyla Yeni Dünyanın Keşfi, Boston katliamı ve Lincoln’nün Gettyburg nutkunun tarihi idi. Peki 2141 ne anlama geliyordu. Bu açıkça dünyanın sonu idi…

Peki işin aslı neydi? Aslında bu bir 1 Nisan şakası idi.

ifadesi gerçekten   için daima ile bölünüyordu. Ancak burda küçük bir matematiksel hile vardı: daima i böler. Şöyle ki:

olsun.

ve

olduğundan ve ile  aralarında asal olduklarından daima

ile ve dolayısıyla tam bölünür.